Disclaimer

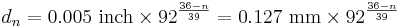
This information HAS errors and is made available WITHOUT ANY WARRANTY OF ANY KIND and without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. It is not permissible to be read by anyone who has ever met a lawyer or attorney. Use is confined to Engineers with more than 370 course hours of engineering.
If you see an error contact:
+1(785) 841 3089
inform@xtronics.com

Wire Gauge - Ampacities - Ampacity

Disclaimer
Wire Gauge - Ampacities - Ampacity

AWG

By definition, No. 36 AWG is 0.0050 inches in diameter, and No. 0000 is 0.4600 inches in diameter. The ratio of these diameters is 92, and there are 40 gauge sizes from No. 36 to No. 0000, or 39 steps. Using this common ratio, wire gauge sizes vary geometrically according to the following formulas.

Where:

d = diameter
n = AWG gauge number
A = cross-sectional area

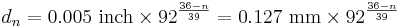
, $d_n = 0.005~\mathrm{inch} \times 92 ^ \frac{36-n}{39} = 0.127~\mathrm{mm} \times 92 ^ \frac{36-n}{39}$

or equivalently

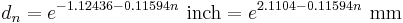
, $d_n = e^ {-1.12436 - 0.11594n}\ \mathrm{inch} = e^ {2.1104 - 0.11594n}\ \mathrm{mm}$

The gauge can be calculated from the diameter using

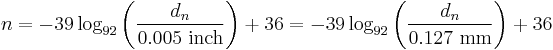
, $n = -39\log_{92} \left( \frac{d_{n}}{0.005~\mathrm{inch}} \right)+36 = -39\log_{92} \left( \frac{d_{n}}{0.127~\mathrm{mm}} \right)+36$

(NB: if you are calculating AWG with a calculator that does not support logarithms to a definable base, then you can apply the Change of Base equivalent equation)

and the cross-section area is

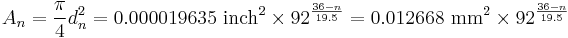
, $A_n = \frac{\pi}{4} d_n^2 = 0.000019635~\mathrm{inch}^2 \times 92 ^ \frac{36-n}{19.5} = 0.012668~\mathrm{mm}^2 \times 92 ^ \frac{36-n}{19.5}$

Sizes with multiple zeros are successively larger than No. 0 and can be denoted using "number of zeros/0", for example 4/0 for 0000. For an m/0 AWG wire, use n = −(m−1) = 1−m in the above formulas. For instance, for No. 0000 or 4/0, use n = −3.

We realize that the use of the legacy inch unit is not optimal - included here due to the historical nature of the wire gage (which should also be discontinued).

Load Carrying Capacities or Ampacities

In part from Reference Data for Engineers: Radio, Electronics, Computer and Communications 7th Ed At 20 C

De-rate with +0.00393 per °C - wire carrying current capacity sitting in the insulation and conduit will not be at 20 °C You will want to derate to at least the temperature rating of your insulation. Resistance listed here are not trade maxima - most wire that is soft or annealed will be slightly higher. Resistance of hard-drawn copper is slightly greater - 2 - 3%. Stranded wire may also be higher.

AWG	Dia Inch	Cir Mil	Dia mm	Area Inch²	lb/kft	ohms /kft	Ohms /km	CU Max free-air Amps	CU Max enclosed Amps
32	0.008	63.2	0.20	4.964E-05	0.19	164.1	538.4	.53	0.32
30	0.010	100.5	0.25	7.894E-05	0.30	103.2	338.6	.86	0.52
28	0.013	159.8	0.32	1.255E-04	0.48	64.9	212.9	1.4	0.83
26	0.016	254.1	0.40	1.996E-04	0.77	40.81	133.9	2.2	1.3
24	0.020	404.0	0.51	3.173E-04	1.22	25.67	84.22	3.5	2.1
22	0.025	642.4	0.64	5.046E-04	1.94	16.14	52.95	7.0	5.0
20	0.032	1,021.5	0.81	8.023E-04	3.09	10.15	33.30	11.0	7.5
18	0.040	1,624.3	1.02	1.276E-03	4.92	6.385	20.95	16	10
16	0.051	2,582.7	1.29	2.028E-03	7.82	4.016	13.18	22	13
14	0.064	4,106.7	1.63	3.225E-03	12.43	2.525	8.284	32	17
12	0.081	6,529.9	2.05	5.129E-03	19.77	1.588	5.210	41	23
10	0.102	10,383.0	2.59	8.155E-03	31.43	0.999	3.985	55	33
8	0.128	16,509.7	3.26	1.297E-02	49.98	0.628	3.274	73	46
6	0.162	26,251.4	4.12	2.062E-02	79.46	0.395	1.296	101	60
4	0.204	41,741.3	5.19	3.278E-02	126.35	0.248	0.8136	135	80
2	0.258	66,371.3	6.54	5.213E-02	200.91	0.156	0.5118	181	100
1	0.289	83,692.7	7.35	6.573E-02	253.34	0.123	0.4035	211	125
0	0.325	105,534.5	8.25	8.289E-02	319.46	0.0983	0.3225	245	150
00	0.365	133,076.5	9.27	1.045E-01	402.83	0.0779	0.2556	283	175
000	0.410	167,806.4	10.40	1.318E-01	507.96	0.0618	0.2028	328	200
0000	0.460	211,600.0	11.68	1.662E-01	640.53	0.04901	0.1608	380	225

A second version of the above table with 60°C trade derating - (affects ohms/kft and ohms/km.)

Max ambient 60°C

AWG	Dia Inch	Cir Mil	Dia mm	Area Inch²	lb/kft	ohms /kft	Ohms /km	CU Max free-air Amps	CU Max enclosed Amps
32	0.008	63.2	0.20	4.964E-05	0.19	199.587	654.613	.53	0.32
30	0.010	100.5	0.25	7.894E-05	0.30	125.521	411.690	.86	0.52
28	0.013	159.8	0.32	1.255E-04	0.48	78.941	258.915	1.4	0.83
26	0.016	254.1	0.40	1.996E-04	0.77	49.647	162.833	2.2	1.3
24	0.020	404.0	0.51	3.173E-04	1.22	31.223	102.407	3.5	2.1
22	0.025	642.4	0.64	5.046E-04	1.94	19.636	64.404	7.0	5.0
20	0.032	1,021.5	0.81	8.023E-04	3.09	12.349	40.504	11.0	7.5
18	0.040	1,624.3	1.02	1.276E-03	4.92	7.767	25.473	16	10
16	0.051	2,582.7	1,29	2.028E-03	7.82	4.884	16.020	22	13
14	0.064	4,106.7	1.63	3.225E-03	12.43	3.072	10.075	32	17
12	0.081	6,529.9	2.05	5.129E-03	19.77	1.932	6.336	41	23
10	0.102	10,383.0	2.59	8.155E-03	31.43	1.215	3.985	55	33
8	0.128	16,509.7	3.26	1.297E-02	49.98	0.764	2.506	73	46
6	0.162	26,251.4	4.12	2.062E-02	79.46	0.481	1.576	101	60
4	0.204	41,741.3	5.19	3.278E-02	126.35	0.302	0.991	135	80
2	0.258	66,371.3	6.54	5.213E-02	200.91	0.190	0.623	181	100
1	0.289	83,692.7	7.35	6.573E-02	253.34	0.151	0.494	211	125
0	0.325	105,534.5	8.25	8.289E-02	319.46	0.120	0.392	245	150
00	0.365	133,076.5	9.27	1.045E-01	402.83	0.095	0.311	283	175
000	0.410	167,806.4	10.40	1.318E-01	507.96	0.075	0.247	328	200
0000	0.460	211,600.0	11.68	1.662E-01	640.53	0.060	0.196	380	225

House Wiring

First, avoid the most common error in house wiring - hanging a 120Vac outlet off of a 3 conductor (L1,L2,N) 220Vac cable. It is dangerous! To do something like that you need a 4 conductor cable - (L1,L2,N,G) to provide a safety ground that is _NOT_ carrying any current.

The table below will not support any reduced ground cables and is for _Copper_wire_only_!. If you run aluminum wire you need to consult the manufacturer's data sheets and be sure to understand terminal block treatments! This table also in no way compensates for length of run! This table is not for wires packed in conduit - wires need to dissipate heat!

Normal COPPER House Wiring Gauge Consult your building inspector because your location will have a specific building code!
Circuit Maximum Amperage	Minimum COPPER wire gage
15A	14AWG
20A	12AWG
30A	10AWG
40A (45A*)	8AWG
55A (60*)	6AWG
70A (80*)	4AWG
95A (100*)	2AWG
Alternate marked * is NOT to NEC code for 60 degree wiring (inside romex). If you are running more than 100A you probably will run Aluminum and need a different table. Do not use copper ratings for aluminum!

UL wire types

UL 1007 - PVC Stranded Tinned -40-105C 300V@80C AWM

UL 1015 - PVC Stranded Tinned -40-105C 600V@80C MTW

UL1018 - PVC 600V@80C

UL 1199 Teflon PTFE insulated

PCB Trace Width vs Current

This chart can diverge from what you see for many reasons.

Fusing Point of Wire

H. W. Preece’s Investigation way back in 1884 provided a way to calculate the fusing current of a wire based on its diameter.

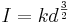
$I = kd^{\frac {3}{2}}$

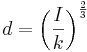
$d = \left ( \frac{I}{k} \right ) ^{\frac{2}{3}}$

Where:

I is the current in Amps

d is the diameter in cm

k is the fusing constant

Material	k for d in cm	Melting point°C	Resistivity (Ω-m) at 20 °C	Coefficient*
Silver	1900	961.78	1.59×10^-8	.0038
Copper	2530	1084.62	1.72×10^-8	.0039
Aluminum	1870	660.32	2.82×10^-8	.0039
Iron	777.4	1538	1.0×10^-7	.005
Tin	405.5	231.93	1.09×10^-7	.0045
Platinum	1277	1768.3	1.1×10^-7	.00392
Lead	340.5	327.46	2.2×10^-7	.0039
Tin/lead solder	325.5	183	1.44x10^-7	.0035

There should be a relationship between resistivity, melting temperature and k. Remember that the electrical resistivity ρ (Rho (letter)) of a material is given by:

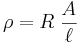
, ${\rho={R \left. \frac{A}{\ell} \right.}}$

where

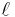ρ is the static resistivity (measured in ohm meters, Ω-m);

R is the electrical resistance of a uniform specimen of the material (measured in ohms, Ω);

, $\ell$ is the length of the piece of material (measured in meters, m);

A is the cross-sectional area of the specimen (measured in square meters, m²).

Watts of heat generated in a wire for a given current

First, an example using the formula in the above section to determine the wattage dissipated in a 1 meter length of 12 gage copper wire at 10A.

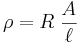
, ${\rho={R \left. \frac{A}{\ell} \right.}}$

Rearrange to solve for R

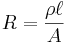
, $R = \frac{\rho\ell}{A}$

Remembering that P = I²R

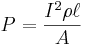
, $P = \frac{I^2 \rho\ell}{A}$

Substituting in where:

I = 10

ρ = 1.72x10^{− 8}Ω − m

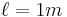
, $\ell = 1m$

d = 0.205cm = .00205m

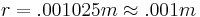
, $r = .001025m \approx .001m$

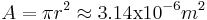
, $A = \pi r^2 \approx 3.14 \mathrm{x} 10^{-6}m^2$

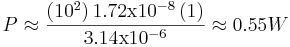
, $P \approx \frac{\left (10^2\right) 1.72\mathrm{x}10^{-8} \left ( 1 \right)}{3.14 \mathrm{x} 10^{-6}} \approx 0.55W$

Temperature Rise in Wire, accounting only for radiative heat loss

Note, in practical terrestrial cases, convective and conductive heat losses will dominate radiative losses. The following are appropriate for only two situations. One, where you have to install cabling in regions with exceptionally thin atmospheres, such as in vacuum vessels or piping. The other, is where the current densities are sufficiently high for the wire to glow - radiative transfer may then dominate the other loss mechanisms and the following can be used.

Now, to figure the temperature rise per watt in steady-state conditions.

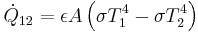
, $\dot{Q}_{12} = \epsilon A\left ( \sigma T_1^4 - \sigma T_2^4\right )$

Where :

, $\dot{Q}_{12} =$ Net radiant energy

ε = emissivity (sometimes called emittance) - the degree of similarity to a black body

ε = 1 a black body

ε = 0.35 a very shiny aluminum alloy

T = Absolute temperature in degrees Kelvin

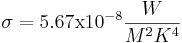, $\sigma = 5.67 \mathrm{x}10^{-8} \frac{W}{M^2 K^4}$ Stefan-Boltzmann constant

When T₁ and T₂ are not very different, it is convenient to linearize the equation by factoring the term , 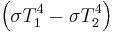$\left( \sigma T_1^4 - \sigma T_2^4 \right )$ to obtain:

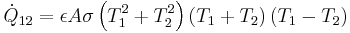
, $\dot{Q}_{12} = \epsilon A \sigma \left( T_1^2 + T_2^2 \right )\left(T_1 + T_2\right )\left(T_1 - T_2\right )$

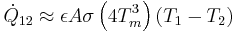
, $\dot{Q}_{12} \approx \epsilon A \sigma \left( 4T_m^3\right)\left( T_1 - T_2 \right )$

When , 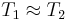$T_1 \approx T_2$ and T_m is the mean of T₁ and T₂

Written again as

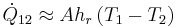
, $\dot{Q}_{12} \approx A h_r \left( T_1 - T_2 \right)$

Where

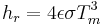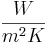
, $h_r = 4 \epsilon \sigma T^3_m$ or Radiation heat transfer coefficient with the units , $\frac{W}{m^2K}$

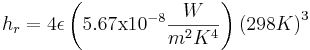
, $h_r = 4 \epsilon \left(5.67 \mathrm{x} 10^{-8} \frac{W}{m^2K^4}\right)\left(298K\right)^3$

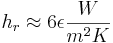
, $h_r \approx 6 \epsilon \frac{W}{m^2K}$

Emissivity is always a fuzzy number that depends on details like surface finish and for copper can vary from 0.7 to .88 but for electrical work 0.4 works most of the time. Give it large error bands!

The surface area of our wire is

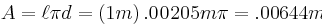
, $A = \ell \pi d = \left(1m\right) .0205m \pi = .0644 m^2$

Our power is 0.55 Watts and , 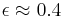$\epsilon \approx 0.4$

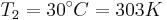
, $T_2 = 30^\circ C = 303K$

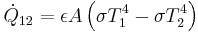
, $\dot{Q}_{12} = \epsilon A\left ( \sigma T_1^4 - \sigma T_2^4\right )$

, $0.55W = \left ( 0.4 \right ) \left ( 0.0644m^2 \right ) \left [ \sigma T_1^4 - \left ( 5.67 \mathrm{x} 10^-8 \frac{W}{m^2 K^4} \right ) \left(303K\right)^4 \right ]$

, $\sigma T_1^4 = \left[ \frac {0.55}{ \left ( 0.4 \right ) \left ( 0.0644 \right )} + 478\right] \frac{W}{m^2}$

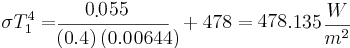
, $\sigma T_1^4 = \frac {0.55}{ \left ( 0.4 \right ) \left ( 0.0644 \right )} + 478 = 480.1\frac{W}{m^2}$

, $T_1 = \left [ \frac{480.1}{5.67 \mathrm{x}10^{-8}} \right]^{\frac{1}{4}} = 303.35K$

or a rise of 0.034 C

We can solve for T₁ generally:

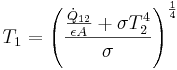
, $T_1 = \left( \frac{\frac{\dot{Q}_{12}}{\epsilon A} + \sigma T_2^4}{\sigma}\right)^{\frac{1}{4}}$

PCB trace width links

Why was 'hot' Black in House Wiring?

Black used to be the colour of the live wire in ordinary cables in Europe (as it still as it is in the USA). This is because the very first power wires were insulated by strips of linen soaked with guttappercha ( a good organic insulator) and natural rubber filled with soot. Hence: black colour for the dangerous one. The neutral wires weren't insulated at all, just bare copper wire. Later they got a grey coating (less soot in them), still later blue as artificial dyes came up in Europe.

Mains wire codes in Germany

In ordinary 230 V AC household cables, e.g. for kitchen devices, TV-sets, small machines etc.:

black live 230 V AC labeled L or L1 or P (Phase, on older devices)
blue neutral, 0 V labeled N
green/yellow protective earth (PE) connected to ground

In three phase 400 V cables

black L1
grey L2
brown L3
blue neutral
green/yellow protective earth (PE) connected to ground.

L1, L2, L3 were labeled formerly as R, S, T respectively. Motor inputs were U, S, V. The corresponding cold ends of the motor windings were called X, Y, Z, usually shorted together in a "star" or "Y" connection arrangement.

In older three phase cables the grey lead was also black so when installing cables, it was difficult to determine the direction of rotation. In cables older than, say, 60 years the PE lead was red, in Switzerland even more recently.

Blue may be (and is frequently) used for any purpose, especially for switched power, can't be sure that it's neutral. Other colours may be used for any purpose. Green/yellow may not be used for anything else but PE.

Other older standards from Europe

In the UK and those areas adopting British standards, red was universally live and black was neutral (with green earth if sleeved)for both fixed wiring and flexes from before the war, until 1971. Then the green with yellow stripe earth was introduced. (mitigating risks of mistake with red green colour blindness) At the same time brown was introduced for live and blue for neutral in new flexes. (3 phase went from red-white-blue to red-yellow-blue, but very few were seriously affected by this. There was also agreement that the colours in this order represent the sequence of positive half cycles for correct rotation. This was a more useful change.) In the UK from late 2005 fixed-wiring also changed to to brown & blue ( this change is sometimes referred to as euro-harmonization). At the same time 3-phase colours went from red/blue/yellow with a black neutral to brown/black/grey with a blue neutral. So now both blue and black can either be live or neutral depending on the age of the installation, leading to some potentially expensive and dangerous errors when old and new systems co-exist.

Prior to Unification in 1989, much of East Germany had many appliances of the older German colour code, with gray and white or black as current carrying colours and red earth. Live and neutral polarity is not preserved in the Shcucko socket system, and it is important to be very careful with older equipment from this era of unknown provenance.

In DC (direct current) electronics applications, Black is most often ground and Red most often positive. More wire about see - telco color codes

Stranded wire Terms

Tinned: Individual copper strands are coated with tin
Heavy Tinned: Similar to basic tinning, but a much thicker coating of tin. It is commonly used with high frequency induction heaters because it can bond on stripped areas while the rest of the cable remains flexible.

Tin Overcoat (TOC): Tinned stranded wire twisted and then is coated with a second coat of pure tin

Top Coat, or Topcoat: Bare (untinned) copper stranded wire is twisted first then gets an overall coating of pure tin. Its advantages are similar to prefused or pre-bond tinning(below). It is accepted by the UL and the CSA, but not the Mil-Spec standards.

Prebonded, Prefused, or Pre-bond: Tinned-Over-Coat or Top Coat that is then fused - which makes it stiffer. They use Heavy tin coated individual wires stranded which are then bonded by resistance heat. (the entire conductor is bonded before other operations, such as insulating, are started.) Acts similar to a solid conductor, but is less likely to break or work-harden in flex applications. Note - some insulated wire manufacturers also use the term "Prebond" to mean any stranded wire which has been fused or overtinned. Prefused or pre-bond conductors are usually accepted under UL and CSA guidelines, but not by Mil-W-16878 cable specifications.

Top Coat, Tinned Over Coat, and Prebonded are often used for wire that goes through a hole in a PCB or terminal block to prevent stray stands from causing shorts. These terms are often misused.