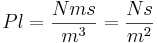
This information HAS errors and is made available
WITHOUT ANY WARRANTY OF ANY KIND and without even the
implied warranty of MERCHANTABILITY or FITNESS FOR A
PARTICULAR PURPOSE. It is not permissible to be read by
anyone who has ever met a lawyer or attorney. Use is confined to
Engineers with more than 370 course hours of engineering.
If you see an error contact:
+1(785) 841 3089
inform@xtronics.com
We can say that viscosity is the resistance a material has to change in form. This property can be thought of as an Internal resistance to flow processes. The word "viscosity" derives from the Latin word "viscum" for mistletoe (A viscous glue was made from mistletoe berries and used to coat lime-twigs to catch birds.)
To get a good feel for viscosity, we need to first digress and remember laminar flow. If a fluid or gas is flowing over a surface, the molecules next to the surface (the ones clinging to the walls) have zero speed. As we get farther away from the surface the speed increases. This difference in speed is a friction in the fluid or gas. It is the friction of molecules being pushed past each other. You can imagine that the amount of clinging-ness between the molecules will be proportional to the friction. This amount of clinging-ness is called viscosity. Thus, viscosity determines the amount of friction, which in turn determines the amount of energy absorbed by the flow.
Imagine a large room filled ankle deep with tar. On top of the tar is a large plate of steel that we want to slide across the surface. Now lets think of the cube of tar under the plate that is resisting this motion.
Friction is a force (in Newtons) acting against the direction of travel. This frictional force scales with the surface area in (in m2). This friction is also inversely related to the thickness of the tar (in m). We all know that it is easier to stir molasses slowly so we know that the force goes up with the speed of stirring (in m/S). With Pl representing our constant of viscosity we derive it here:
Force = Pl x (Area of plate) x (speed) / (thickness)
Changing speed to Distance per second distance / time :
Force = Pl x (Area of plate) x (distance) / (thickness) x (time)
Rearranging to solve for the Poise value for tar:
Pl = Force x (thickness) x (time) / [(Area of plate) x (distance)]
or:
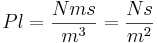
This is viscosity; a unit of power per unit of area, unit of speed
and unit of speed gradient. ([#twist see this])
The Abbreviation Pl is the SI (mks) unit is called a Poiseuille. Unfortunately, no one uses it; instead they use the old cgs version of this formula expressed in dyne-seconds per cm2 which is called a Poise (it is smaller, thus shorter (;-). Actually, industry uses the centa-Poise or one-hundredth of a Poise because water has a viscosity of 1.002cP which is very close to 1.
So one Poiseuille = Ns/m2 = Pa*s = 10 aPoise = 1000 cP
,

|
The names Poiseuille and the shortened Poise are from the great French physician, Jean Louis Poiseuille (1799 - 1869). I will digress at this point to try and help you pronounce this unit's name the best I can. Unfortunately, like many of the French, he had a name that is impossible to pronounce or spell. (The problem of pronouncing Poiseuille may well be the main cause of the United States failing to embrace the metric system<grin>) To start with poise is NOT pronounced as its homograph poise, meaning to walk in a balanced, dignified manner. Instead, imagine you are all puckered up, ready to kiss, just as your partner stomps painfully on your toe. The sound that comes out is "Poise". Phonetically it is spelled pwaz. (Hint: Be sure to practice in a place where you won't accidentally spit on someone.) With a little practice you will have mastered the more common of the units. Don't worry if you don't say it quite correctly; no one else can either or will ever even know the difference. Now for those up to a bit of a challenge; "Poiseuille". The first syllable is the same as Poise. All that is left is uille. A big help when pronouncing French words is to ignore the sounds of the all the letters. The syllable uille has no U, I, L, or E sound. Fill your mouth full with extra viscous peanut butter, plug your nose, and say sores. Phonetically it is spelled z Ə (r)z Probably because no one could pronounce his name, Poiseuille became a hard working student. Schooled in physics and mathematics Poiseuille developed an improved method for measuring blood pressure. Poiseuille’s interest in the forces that affected the
blood flow in small blood vessels caused him to perform
meticulous tests on the resistance of flow of liquids
through capillary tubes. In 1846, he published a paper on
his experimental research. Using compressed air,
Poiseuille forced water (instead of blood due to the lack
of anti-coagulants) through capillary tubes. Because he
controlled the applied pressure and the diameter of the
tubes, Poiseuille’s measurement of the amount of fluid
flowing showed there was a relationship. He discovered
that the rate of flow through a tube increases
proportionately to the pressure applied and to the fourth
power of the tube diameter. Failing to find the constant
of proportionality, that work was left to two other
scientists, who later found it to be ,
(This story is somewhat misleading because blood flow pulsates and the viscosity of blood declines in capillaries as the cells line up single file. Thus, even with this information we have to wait for the discovery of anticoagulants - (by a long hair, Karl Paul Link, at University of Wisconsin -- vitamin K) to do definitive experiments.) |
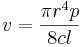
While the viscosity of solids and liquids falls with increasing temperature (inverse relationship), the viscosity of a gas increases. While it seems counter intuitive, the rise in gas viscosity as a function temperature can be understood. As a gas gets higher in temperature it has more collisions, and thus, more friction with its neighboring molecules.
Another surprise is that pressure has very little effect on the viscosity of water. Waters virtual independence from pressure means that water flowing in a pipe has an insignificant change in friction whether at 60 psi or 20,000 psi!
Water is uniquely self compressed by hydrogen bonding. At a
molecular weight of 18, it is lighter than air and otherwise would
be concentrated at the outer limits of the atmosphere. To
understand this compare water to the iso-electronic, and heavier,
gas H2S.
Instead, water is a liquid because its tetrahedral arrangement of
two protons (positive charges) and two electron pairs (negative
charges) makes the molecule polar which causes collections of
water molecules to spontaneously arrange themselves into
assemblies held together by electrical charges. This hydrogen
bonding force or 'Van der Waals' force is somewhat greater than
several thousand psi we might apply.
Oils, and almost everything else, are not so self-compressed.
Paraffinic oils, in particular, are held together by much weaker
induced dipole charges. Thus there is much space between the
molecules that allow them to pass easily by each other. This space
can be reduced by applying pressure, increasing density and
viscosity.
This difference is of critical importance to the business of
drilling for oil. When an 8" hole, 4 miles deep is filled with
water, the viscosity is essentially the same from top to bottom.
When filled with oil, viscosity and density varies from top to
bottom, making it much more difficult to predict friction
pressures of flows.
So water and gas's viscosity are mostly independent to pressure. With Gases until the pressure is less than 3% of normal air pressure the change is negligible on falling bodies.
The Poiseuille and the Poise are units of dynamic viscosity sometimes called absolute viscosity.
1 Poiseuille (Pl) = 10 poise (P) = 1000 cP
P = 0.1Pl
1 centi-Poise (cP) = .01 poise
| Some examples of Viscosity - these may help
you get a feel for the cP Send in number if you have them |
|||||
|---|---|---|---|---|---|
| Hydrogen @20°C | 0.008 6 cP | Benzyl ether @ 20°C | 5.33 cP | Honey | 3,000cP |
| Ammonia @ 20°C | 0.009 82 cP | Glycol @ 20°C( probably ethylene glycol) | 19.9 cP | Honey @ 20°C | 10,000 cP |
| Silane SiH4 1.013 bar and 0 °C |
0.0108cP |
|
|
|
|
| Water vapor @100°C | 0.012 55 | Linseedoil (Raw) | 28cP | Honey | 2,000-3,000cP |
| CO2 gas @ 0°C | 0.015cP | |
|
|
|
| Air @ 18°C | 0.018 2 cP | Linseedoil (Boiled) | 64cP | |
|
| Argon @ 20°C | 0.022 17 cP | Soya bean oil @ 20°C | 69.3 cP | |
|
| Air @ 229°C | 0.026 38 cP | Corn oil | 72cP | |
|
| Neon @ 20°C | 0.031 11 cP | Olive oil @ 20°C | 84.0 cP | Blackstrap Molasses | 5,000 - 10,000cP |
| Water@20C | 1 cP |
|
|
|
|
| CO2 Liquid @ -18°C | 0.14cP | |
|
Molasses @25°C | 8,700cP |
| Liquid air @ -192.3°C | 0.173 cP | Light machine oil @ 20°C | 102 cP | ||
|
|
|
|
|
molten Glass | 10,000cP |
| Ether @ 20°C | 0.233 cP | Motor oil SAE 10 (ISO 32) |
50-100cP 65cP | Chocolate syrup @ 20°C | 25,000 cP |
| Water @ 99°C | 0.2848 cP | Motor oil SAE 20 (ISO 46-68) |
125cP | Hershey’s Chocolate Syrup | 10,000-25000cP |
| |
|
Motor oil SAE 30 (ISO 75) |
150-200cP 200cP | Ketchup @ 20°C | 50,000 cP |
|
|
|
Motor oil SAE 30?? | 100cP |
|
|
| Acetone | 0.3cP | Motor oil SAE 40 (ISO 150 ) |
250-500cP 319cP | Ketchup Heinz | 50,000 - 70,000cP |
|
|
|
70% Sucrose in water | 480cP |
|
|
| Benzene | 0.50cP | Motor oil SAE 50 | 540cP | Ketchup @25°C | 98,000cP |
| |
|
Heavy machine oil @ 20°C | 233 cP | Peanut butter | 150,000-250,000cP 250,000cP |
| |
|
Caster oil @ 20°C | 986 cP | Corn Syrup | 110,000cP ?? |
| |
|
Motor oil SAE 60 | 1,000 - 2000cP 1,000cP | Peanut butter @ 20°C | 250,000 cP |
|
|
|
|
|
Soft end of glass working range | 1.0x106cP |
| Chloroform@ 20°C | 0.58 cP | Glycerin @ 20°C | 1,410cP 1,490 cP |
Smooth Peanut butter @ 25°C | 1.2x106cP |
| Methyl alcohol@ 20°C | 0.597 cP | Motor oil SAE 70 | 1,600cP | Bitumen Canada’s Athabasca reservoir sands are about 10-12% bitumen, at 11 deg. C | 1 x 106 cP |
| Benzene @ 20°C | 0.652 cP | Pancake syrup @ 20°C | 2,500 cP | Crisco Shortening | 1x106-2x106cP 1.2x106cP |
|
|
|
|
|
Glass Softening Point (sags of own weight) | 3.9x106cP |
| Water @ 20°C | 1.002 cP | maple syrup @25°C | 3,200 cP | Window putty | 1x108cP |
| Ethyl alcohol @ 20°C | 1.2 cP | Venezuela’s Orinoco extra heavy oil reservoirs are about 53 deg. C with viscosity of | 1,500-3,000 cp | Firm end of glass working range | 1x1010cP |
|
|
|
|
|
Tar or pitch @ 20°C |
3x1010cP |
| Mercury @ 20°C | 1.554 cP | 1x1010cP | |
Soda Glass @ 575°C | 1x1015 cP |
|
|
|
|
|
Glass Annealing point | 1x1015 cP |
|
|
|
|
|
Glass Strain Point (low end of annealing process) | 3.1x1016 cP |
| |
|
|
|
Earth upper mantle |
3 to 10*1023 cP |
| |
|
|
|
Earth lower mantle |
2 to 3x1025 cP |
If there are two numbers listed above it refers to two difference
sources of the information. None of the source measurements had
any error number associated with them.
SAE motor and SAE
gear use different numbers.. better to use ISO
Nice thing about standards is ... there are so many to chose from ..
SSU or Seconds Saybolt Universal. It is the amount of time
in seconds required for 60 milliliters of liquid to flow through a
calibrated orifice under controlled conditions as per ASTM D 88.
This method has largely been supplanted by the kinematic viscosity
method. [thankfully]
To obtain the Saybolt Universal Viscosity equivalent to a
kinematic viscosity determined at t, multiply the equivalent
Saybolt Universal Viscosity at 100°F by 1 + (t - 100) 0.000064.
Example: 10v at 210°F are equivalent to 58.91 multiplied by 1.0070
or 59.32 sec Saybolt Universal at 210°F.
Degree MacMichael (°McM) a unit used to measure the viscosity, or thickness, of chocolate. Typical values range from around 60 °McM (very thin chocolates suitable for pouring into molds) to around 190 °McM (very thick chocolates suitable for hand dipping or forming around a center). A MacMichael viscometer is used to make the measurement.
Two different conversions to MacMichael --
Brookfield ???
Please update with any conversions between Brookfield and
centa-Poise or Machmichael and centa-Poise
The Poise is not related to density. To come up with a unit incorporating density we look at the Poiseuille divided by density. Remember that a Poiseuille is a Newton-second per square meter or ns/m2. Remembering that a Newton is a Kilogram - meter per second squared or kg m/s2
we can re write the Poise unit as kg m s/m2s2
which simplifies to kg/ms. Corresponding units for density
would be the Kilogram per cubic meter or kg/m3 so
dividing a Poise Unit by density gives us
kg m3/kg m s which simplifies to m2/s. The
common kinematic viscosity unit is the Stokes, abbreviated
St. Instead of being in SI units, the stoke is in
cgm units of cm2/s and one ten-thousandths the size.
,

|
George Stokes' law of viscosity established the
science of hydrodynamics. We most often run into him with
the work he did on the settling of spheres, but he also
derived various flow relationships ranging from wave
mechanics to viscous resistance.
Stokes papers on the motion of incompressible fluids, the friction of fluids in motion, and the equilibrium and motion of elastic solids exemplifies his wide range of influence in physics. His works on the transmission of acoustic waves through viscous materials (like tar) are also of interest. Stokes also investigated the wave theory of light, named and explained the phenomenon of fluorescence, and theorized an explanation of Fraunhofer lines in the solar spectrum. He suggested these were caused by atoms in the outer layers of the Sun absorbing certain wavelengths. However when Kirchhoff later published this explanation Stokes disclaimed any prior discovery. In short Stokes was an all-around whiz kid (whose name we can pronounce). (If you know of any good stories about George email them here). Stokes came up with a formula that can predict the rate at which a sphere falls through a viscous gas or liquid. He was the first to understand why a mouse can fall 1000 feet and walk away yet a man would be dead. |
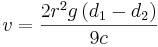
This velocity is the terminal or ultimate velocity the sphere will attain falling through the liquid or gas in question. Thus approximating a mouse and man’s body as a sphere, and assuming that we have a radius 5 times that of a mouse – the terminal velocity of a man (about 100 mi/hr) would be 25 times that of a mouse! This form of the equation can be solved for Poise and the experiment timed (to determine terminal velocity) so that we have a handy way to measure viscosity.
Dropping a sphere of known size and mass in a liquid and measuring its terminal speed is one way to measure viscosity. This method gives an enormous range of measurements; the largest to smallest readings give us a ratio of about a billion to one. Noting the temperature is most important when taking such a measurement because of the great change even a small change in temperature can cause. Caster oil can change its viscosity about 8% per degree c!
The equations covered so far work as long as the motion is slow enough to keep the flows in the laminar domain. Once the speeds increase past a limit the drags grow at enormous rates. Sometimes it is necessary to figure out if the dominant variable is the viscous flow or inertial flow.
,

|
There is no way to do justice in describing Reynolds work; that would require a book. He was not just a scientist, but also the prototype of the modern engineer. In his work can be seen the rigorous error checking that set the standards for later workers. Although Reynolds is best known for his number, few fields of science and engineering are not touched with his life’s work. From discharge tubes, to bearings, to thermodynamics, to cavitation, to magnetism, and electricity; he left his mark. (Yet, this is but a part of what he did!) This Irish Brit -- Osborne Reynolds -- came up with a unit that like the Mach number is dimensionless. When the Reynolds number (abbreviated Re) is properly calculated all units cancel out. |
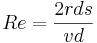
(all units cancel out),
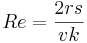
Small Reynolds numbers mean that the fluid's viscosity is dominant. On the other hand when Re is larger than 10,000 it means that viscosity is negligible and the kinetic or inertial effects rule.
When Re is high, turbulence, cavitations, and chaos describe the flow. When Re is low, laminar flow dominates and drag is approximately equal to speed X size X dynamic viscosity giving a linear rise in drag with speed (and a squaring of power with speed).
On the other hand, when Re is large drag is approximately equal to Speed2 X Size2 X density! This means that once the Reynolds number is large, drag goes up with the square of speed and power goes up with the cube of the speed!
A kind reader noticed (from an older version of this page) my failed attempt at explain viscosity (I tried to make the equation to mean a unit of power per unit of area - something it is not). My goal was to put viscosity in to an intuitive concept using an energetic approach to grasping the units. My Idea was that viscosity could be seen as the ability to absorb power.
The classic definition for viscosity which you have put in the current version of your page is:
Viscosity = [Frictional Force x thickness x time] / [(Area of plate) x (distance)] I would like to group this expression in a slight different manner, to show the physical meaning of viscosity:
Viscosity = [Frictional Force/Area of plate] / [(distance/time)/(thickness)]
The last part of the expression is the concept “speed variation for thickness unit” (actually the speed gradient in a direction perpendicular to flow). So, the dynamic meaning of viscosity would be:
Viscosity is the force needed to apply on a plate of unit surface in direction of travel to move it to achieve a unitary speed variation for each unit thickness.
Or the same using differential analysis elements:
Viscosity is the force needed to apply on a plate of unit surface in direction to travel to move it to achieve a unit of speed gradient.
Now let as go to an energetic approach to viscosity.
Power (P) is force times speed.
Power = Force x speed
But frictional force is, according to dynamic formula:
Frictional force = [Viscosity x Area of plate] x [(distance/time)/(thickness)]
so, power is:
Power = speed [Viscosity x Area of plate] x [(distance/time)/(thickness)]
and the energetic expression of viscosity is now:
Viscosity = Power / {Area of plate x speed x [(distance/time)/(thickness)]}
Being the viscosity definition:
Viscosity is the power needed to apply on a plate of unit area to sustain a unit speed keeping a unitary variation of speed for each unit thickness.
Or using differential analysis expressions:
Viscosity is the power needed to apply on a plate of unit area to sustain a unit speed with a unit speed gradient.
So, using dimensional analysis:
“This is viscosity; a unit of power per unit of area, unit of speed and unit of speed gradient” Hugo J. Gavarini
Reynolds number! I haven’t heard much about that since I was at the wind tunnel. Simulating the proper Reynolds number in a wind tunnel has always been a problem with scale models. One approach is a pressure tunnel. By increasing the pressure in the tunnel to increase the density or use a gas other than air that is more dense. As the tunnel runs it tends to heat up which works against you by lowering the density. The Vertol tunnel had an air exchange system to keep the tunnel cool. To simulate a higher Reynolds number we tripped the boundary layer at the appropriate point on the wing to transition to a turbulent boundary layer. This was done with a narrow band of grit glued to the wing surfaces. We also used small vortex generators glued to the wing to put the appropriate amount of energy into the now turbulent boundary layer. KFS Wichita
In the book "Theory and Practice of Lubrication for Engineers" by Dudley D. Fuller, he states that pressure has a significant effect on viscosity for lubricating oils. For example he shows that it may change by a factor of 2 when the pressure changes from atmospheric to 3000 psi. Is Fuller correct?
D Lund
Hello, Hey, you really have a great web page on viscosity! One of the challenges I have as an oil well drilling engineer is trying to explain viscosity and its effects on the friction pressure. When you have long well-bores, and you try to pump fluids in (or out), the friction pressures can be in 100’s or 1000’s of psi. If the friction pressure gets too high, subsurface formations may break down, and the fluid may go where you don’t want it to. Lisa Denke Diatomite Drilling Engineer
-
very nice explanations!... the Re number for expelled lung mucus is about 100...so is this a high number bordering on Newtonian Physics or a low number in non-newton territory given that beating cilia (seried ranks of 200 of them over 25 square microns) act on the mucus at 10 Hz anil mehtaEmail
(C) Copyright 1994-2019
All trademarks are the property of their respective owners.