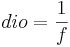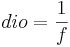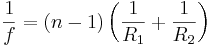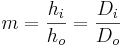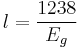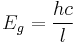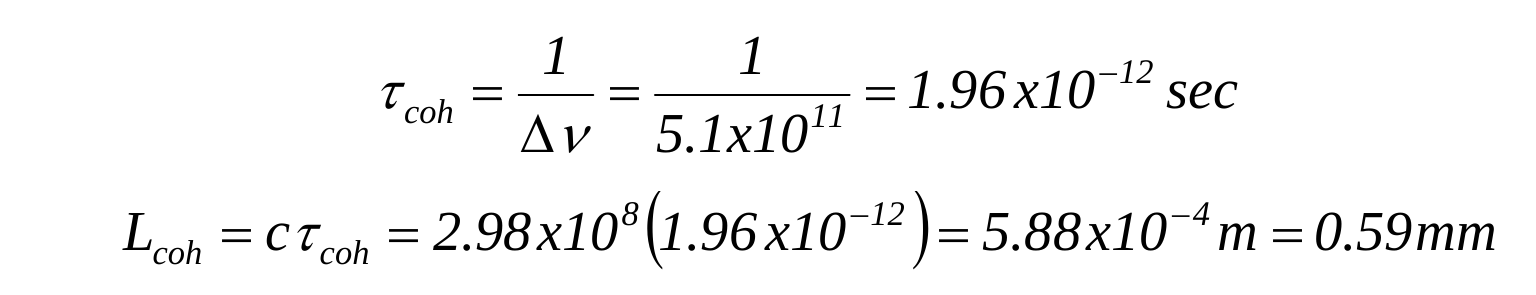Disclaimer

This information HAS errors and is made available WITHOUT ANY WARRANTY OF ANY KIND and without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. It is not permissible to be read by anyone who has ever met a lawyer or attorney. Use is confined to Engineers with more than 370 course hours of engineering.
If you see an error contact:
+1(785) 841 3089
inform@xtronics.com

Optic equations and notes

Disclaimer
Optic equations and notes

Diopter or Dioptre

The diopter unit is simply the inverse of the focal length in meters.

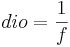
$dio = \frac{1}{f}$

Thus a +2 diopter lens has a focal length of 500mm

You can combine lenses of different diopters arranged in contact - thus a -2 diopter lens plus a +4 diopter lens would give us the same 500mm focal length.

Focal Length

If a lens has surface radii of R₁ and R₂ and made of glass with an n refractive index the focal length, f, is defined below

R₁ and R₂ = surface radii (negative for convex lens surface)

n_g = refractive index of the lens glass

f = focal length of lens

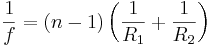
$\frac{1}{f} = \left(n - 1\right) \left(\frac{1}{R_1} + \frac{1}{R_2} \right)$

Focal length to angle of view

α = angle of view d = size of film or sensor f = focal length

Depth of Field

Depth of Field is the minimum to maximum distance in focus.

Contrast Ratio

Contrast ratio is the difference between the brightest and darkest point in an image.

Lens power or Magnification ratio

Where

m = Magnification ratio or Power

h_i = image height

h_o = object height

D_i = distance from lens to image

D_o = distance from lens to object

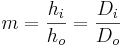
$m = \frac{h_i}{h_o} = \frac{D_i}{D_o}$

Spherometers - lens Radius from arc depth

Calculating lens Radius from arc depth

C of the Triangle is the same as Radius.

The bottom has a calculation of the Spherometers leg from the radius.

Variables in light optics Greek

V = frequency in hz

ω = radian frequency

δ = path difference (corrected for n)

φ = phase difference

P = order of interference = K

e = thickness

τ = coherence time

l = coherence length

n = index of refraction

a = distance from center

Phase reversal on reflection

Light phase flips (E-field only) when reflecting off a material with higher refractive index than what it is traveling through.

Brewster angle reflections have no phase change.

If light reflects off an internal wall of a prism or flat - phase does not reverse.

Phase reversal is important when analyzing coatings.

Rayleigh Water Test - for testing optical flats

Monochromatic light source (not LED) - neon/ mercury vapor sodium
Leveling platform - fine pitch screws - differential would be best - but long allen wrench - with long cheater in cap screw
A lens bigger than the flat - collimator - Fresnel a good bet.
Black tray - should not rest on bottom of tray?
Draft preventer - Coraplast taped together
stable surface - no vibrations - Concrete - add weight to platform
LASER pointer
Magnifier might help see small bands.
Best water thickness over glass - .9mm± .2mm - A dime is a bit too thick - but will get you close..

Rayleigh-water-test

The interference creating bands happens between the water surface and the top of the glass.

Back to the water test - I'm still not seeing what I want to - I've started experimenting - trying to see a pattern with a single microscope slide - the reflection from the front and rear surface seems close to the water test. (The double slide glass interference is easy).

To see the single glass, the light and eye want to be very close together - a normal view point to the surface - It

Getting things level is the hardest bit - point a LASER pointer straight down - align the dots - and hope you get close. The LASER should be directly above and aimed so the dots are close to the LASER - 10mm or less.

The drill is to look without the collimating lens in place - you want to find rings - adjust so they are wide.. If the rings are close - a magnifying glass might help. Focus on the image of the lamp - that is where you will see the first lines. (This didn't seem to work well - very careful LASER alignment was more important).

The leveling screws I used were differential - made from a M8-1.25 capscrew that was drilled out to mount a M6-1.0 - the thread difference gives 250um per turn.

Fringes formed from a non uniform film (wedge) are called Fizeau fringes.

Newton rings are a type of Fizeau fringe - the wedge being concentric from being pressed together at a point.

Haidinger fringes are fringes of equal inclination - pin hole source best viewed with a large aperture lens. (longer path length means coherence length is critical).

Wavelength of LED or Laser based on band-gap voltage

The wave-length in lens specifications is 632.8nm - helium-neon LASER - (Comes from a persistent neon line -- with low concentrations of a particular element relative to other substances in the source, the number of observable lines decrease with decreasing concentration until only the most persistent remain. Should have been called a Neon-Helium LASER) but other monochrome light sources are available - LEDs and LED LASERs

Below is an estimation based on the voltage drop which is close to the band gap of a forward biased diode.

l = wave length in nm

E_g = band-gap voltage

then

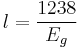
$l = \frac{1238}{E_g}$

Thus those red LEDs with a 1.9V drop run about 652 nm. (GaAs_0.6P_0.4)

This appears derived from , 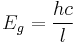$E_g = \frac{hc}{l}$
Where:

h = Plank's Constant = 4.13 x 10-15 eV·s

c = speed of light = 2.998 x 108 m/s

Colors of wave lengths

Infrared 710nm and goes down to roughly 2000nm.

The visible range is considered to be roughly 400nm to 710nm.

390nm to 420 is Blue (or Violet),

530nm is green

Mercury e-line = 546.07 nm

589nm - sodium D lines - a doublet - two lines 589.0 and 589.56nm - coherence length 0.59mm (must be one line) (588.9950 and 589.5924)

600nm to 710nm is considered red.

632.8nm - helium-neon LASER - neon - bandwidth about 0.002 nm compared to LED bandwidth of 24-27nm - 10,000 wider.

Refractive Indexes 632nm

Fused silica 1.457

Fused Quartz 1.46

Zerodur 1.542

Borofloat 1.472

Clearceram-Z 1.54

ULE 1.48

N-BK7 1.51

Water ~ 1.33

Coherence time and Length

Example of Coherence Length
Sodium vapor lamp yellow "D" line
• λ = 589 nm and line-width 5.1x1011 Hz
• Thus coherence time and length is

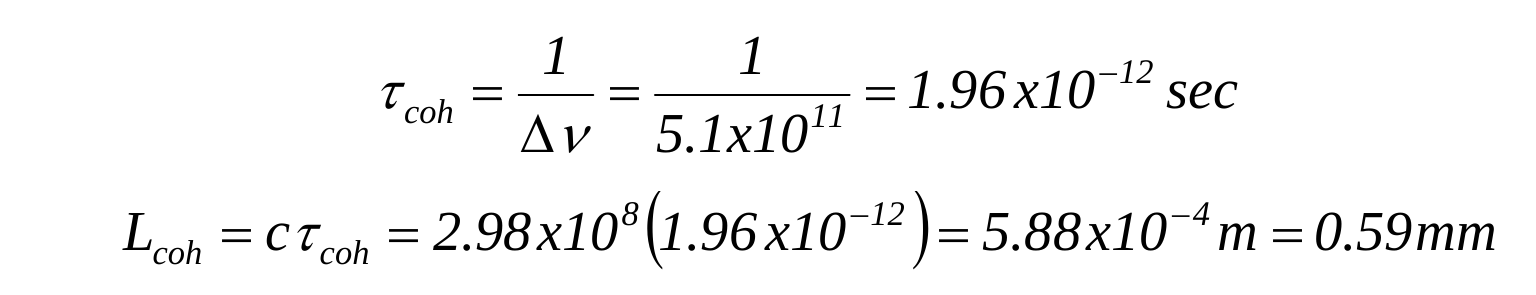
The mercury line at 546.1 is .3mm ?? varies greatly with tube pressure

Coherence length test

A pen LASER has a coherence length of about 10mm - because the slide is thinner there is an interference pattern on the screen. If in place of the slide there was a 15mm optical parallel - the pattern fails.

Interferometers

Bath Interferometer

The Bath interferometer is not effected by coherence length. A bit of a puzzle why? The trick is to think in time - rather than length - thus coherence time - and to focus on correlation. Light interference requires the light to be correlated in (average) phase (and to have some amount of spacial coherence as well).

So for a Newton rings - a type of Fizeau fringe - the time it takes to travel the two paths - is different - varies in time. Thus if the source has a short coherence time - and the difference is greater, the interference pattern falls apart. When the light arrives - it is no longer correlated even if at an even cycle time of the given light frequency.

But for the Bath - the time difference of the path is never greater than the defects of the mirror under test - those defects would have to be greater than the coherence length for it to fall apart. (Imagine a mirror surface with a 10mm defect - the absurdity makes it memorable <grin>)

The light doesn't care about time varying phase - as long as it is correlated between the two sources. So if you imagine that the light source was oscillating in phase like an FM radio station - limiting the coherence time to part of one of these cycles - it doesn't matter - the light creating the pattern has the same phase when it arrives. Coherence time means that phase changes in time - not because it traveled some length - both beams started off the same - have the same path length - so will arrive the same as well. Both arrive highly correlated. So coherence length matters if the time of flight differs - the key detail.

The following I think came from Dale Eason - couldn't find the original link.

Best Practices

The software requires a good “igram” for input – a photograph of the interference fringes due to interference of the test and reference beams. These guidelines are meant to supplement Dale’s instructions with a “Best Practices” for obtaining high quality, clean igrams. Much of this material is dispersed throughout years of posts in the messages section.

XYZ stage - A stable, smoothly controllable xyz stage is critical to avoid frustration and wasted time in taking igrams. This can be purchased, for example on ebay, or made (see “A simple to make Bath and xyz stage” in the Wiki for an example). Precisely repeatable adjustment as in the wire or caustic test is not required, just smooth and stable fine adjustment
Firm foundation - A firm support for the stage and mirror test stand, such as a concrete slab floor, are also required. A wood floor generally moves as you shift your weight causing the fringe pattern to shift. Worst case it may completely disappear when you move away from the xyz stage after making adjustments. Also, optical components should be firmly fixed in place, so they do not move when making stage adjustments.
Mirror test stand - Using 3 “stops” to define a plane to place the back of the mirror against in the test stand will facilitate repeatable positioning of the mirror test session-to-test session. This works best with two rollers supporting the mirror, one 45 deg cw (clockwise), the other 45 deg ccw from the bottom of the mirror, with their axes of rotation parallel to the plane of the mirror back. No difference in test results was seen between this type of support and a 'whipple tree' linkage with rollers at +/- 27 deg from the two 45 degree points for a 22.4" diameter x 2" thick quartz mirror, i.e. any difference was within the noise level comparing averages of 30-50 wave-fronts. A tad of "toe-in" of the rollers helps keep the mirror back against the 3 support points. The reflected test and reference beams will then be very close to the same position each time so that only adjustment of the xyz stage is required to obtain fringes, with no movement of the tripod or whatever you use to hold the stage. You can usually find the beams by holding a screen in front of the flat mirror since they won't be far out of alignment, and with the above type of test stand support the only adjustment required will be using the vertical (z) and horizontal (y) motion of the stage to center the beams, provided you didn't move the diverging lens or other optical components from their position during the last measurements. Once aligned this way, with the reference beam centered on the test beam, you can then move the camera back, hold the screen there and more finely adjust so the reference beam covers the test beam. It typically takes less than two minutes to place the mirror and adjust the y and z positions (x taken as parallel to the optical axis) to get good fringes and be ready to take igrams. Some tweaking of the x position may also be required to adjust the number of fringes on the mirror. You then of course have to wait for the mirror to equilibrate in temperature.
Bath to test mirror distance - A diverging lens position just inside the test mirror radius of curvature generally works well. The two beams generally come to focus somewhere inside the beam splitter. You can fasten a wood block or similar on your mirror test stand aligned below the mirror center, then run a tape measure from it to the Bath lens to check distance. Usually the Bath is mounted on a tripod for rough vertical adjustment. Move the tripod for initial rough set up of the Bath-to-test mirror distance.
Alignment of beams - The test and reference beams should be approximately parallel to each other. This can be done anywhere using a piece of cardboard for a screen. The screen can be placed much further away than the mirror will be during testing to aid in good alignment. The diverging lens is moved aside when aligning the beams.
Beam separation - The distance between the two beam paths results in some field astigmatism (a property of the surface being tested). Place the flat mirror so it is almost touching the bs in a right angle Bath so that you can position the reference beam on it with less than ~ 8 mm spacing from the test beam, to minimize Bath-induced astigmatism. The main limitation on beam spacing will be the cross section of the beams which determines how close you can place them to the corner of the cube splitter on a right angle Bath. This also effects how large a lens you require to be able to relatively easily get both beams fully captured by it. A 6mm diameter lens was originally recommended, but it can be difficult to get both beams aligned in a 6mm lens. Up to 8 mm diameter seems to work fine on most mirrors, even 9mm. DFTFringe can estimate the Bath and test stand-induced astigmatism, and testing the mirror at different rotation angles and averaging the results removes this source of astigmatism. See Notes about Bath interferometer in the Wiki for a discussion of Bath astigmatism. Note that not uniform air density in the optical path can also induce astigmatism, so always rotate the mirror and test again to see if the astigmatism is in the mirror or due to air density distribution. The latter can sometimes be quite a problem, see below.
Position of diverging lens - After aligning the beams the diverging lens must be adjusted so the test and reference beams pass through its center. Misalignment can result in non-uniform illumination of the test and/or reference beam resulting in high unwrap errors and wave front distortion. Then hold a white screen where the camera normally will be, and observe the test and reference beams and adjust the diverging lens position until the test beam image of the mirror is round, and it and the reference beam are both uniformly illuminated. This is critical for good igrams.
Laser wavelength - Laser wavelength should be measured for more accurate results. A number of people have described using a diffraction grating for this. An example is given in the Wiki section Measuring laser wavelength.
Rotating the laser - The laser beam is usually polarized so rotating the beam (electric field) changes reflection at optical surfaces and effects the splitting by the beam splitter (BS). Rotate the laser to determine what angle gives the most uniform beam and highest contrast in the fringe pattern by observing the fringes through the camera as you rotate.
Test and/or reference beam inhomogeneities - The laser diode beam can have dark areas or “spots”, or “mottling” which can cause unwrap errors and result in large spikes in the wave-front. Expanding the laser diode beam by placing the diode at the focal point of a collimating lens and placing a 2mm to 4mm hole in front of, and centered on the lens can greatly improve beam homogeneity. The laser diode lens (if any) is removed in this case. This also generally results in a large, round reference beam, 2 to 3 times larger than the test beam when viewed on a screen. This greatly facilitates slight misalignment of the beams (“tilting”) to adjust the number of fringes across the mirror image without getting the mirror test image partly in a darker area of the test beam. This is more likely to occur with an unexpanded, elliptical or “rectangular” test beam and may result in such high unwrap errors that the igrams are useless.
Many times mottled areas are just due to dust on the optics. It is important to keep all optical surfaces clean to avoid dark spots on igrams. Eyeglass lens cleaner and cloths work well. You can simply slide a plastic bag over the Bath to keep dust off when not in use.
Spurious fringes (fringes caused by reflections from the optical surfaces) - Antireflective (AR) coating of the diverging lens and the beam splitter (bs) can greatly reduce or eliminate these. They can be quite distinct with uncoated optics, resulting in very high unwrap errors – 3k to 7k and useless wave fronts. They can sometimes be moved off to the side enough to get usable igrams by rotating the bs a bit, but this may not be possible. If you rotate the bs, remember you have to re-align the beams. Rotating the interference fringe pattern so the fringes are about normal (perpendicular) to the spurious fringes can significantly reduce unwrap errors, but they may still be greater than 1k to 2k.
Fringe print through - The fringe pattern may sometimes be seen in the wave front as a series of ridges in the shape of the fringes. Usually reducing igram brightness will reduce these (say reducing exposure from 1/80 sec to 1/100 sec depending on your camera/lens and laser diode power). Fringes should be just bright enough for you to see the edges to place the mirror outline. Taking igrams at two different fringe orientations on the mirror will usually eliminate fringe print through.
Distortion due to air currents and/or stratification - A tunnel generally reduces air currents, reducing distortion of wave fronts. A heavy fabric like canvas, or a rigid material like a cardboard concrete form that resists movement aids in this. Running a fan to homogenize air in the tunnel can reduce air stratification, greatly improving wave front smoothness. Run it for just 20 seconds or so to homogenize the air, wait a about 10 seconds or so (at around 80 F) for the air to settle a bit, then start taking igrams. The colder the air the longer it takes for it to settle.
Testing in cold air, special considerations A tunnel is essential to minimize air currents due to thermal mismatch between nearby surfaces and the cold air. Long times are required for the mirror to come to thermal equilibrium. A fan cooling the mirror will greatly reduce this time, but it may still take several hours depending on the difference in temperature of your mirror figuring area and the test area. It has been observed that wave fronts obtained after about 3 hours may differ a bit from ones taken the following morning, with the center generally shorter compared to the edge in the wave fronts obtained after 3 hours. Again, depending on temperature difference in figuring and testing areas. If testing in cold air, minimize the time you are close to the tunnel entrance because air warmed by your body will move into the tunnel causing air stratification and distortion of wave fronts. When testing in cold air, difference in floor temperature and air temperature drives air currents, making it almost impossible to obtain undistorted wave fronts. Covering the floor area inside the tunnel with foam or other insulating material will greatly reduce this effect.

Fast Lenses

Translated from French http://www.dg77.net/photo/tech/fast.htm

to add post it here!

Top Page

wiki Index