Disclaimer

This information HAS errors and is made available WITHOUT ANY WARRANTY OF ANY KIND and without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. It is not permissible to be read by anyone who has ever met a lawyer or attorney. Use is confined to Engineers with more than 370 course hours of engineering.
If you see an error contact:
+1(785) 841 3089
inform@xtronics.com

Mass Flow by square root extraction

Measuring the flow of fluids with an orifice plate

Sometimes we want to measure the flow of a material that isn't happy going through an impeller (or we might want to avoid having to maintain the shaft seal). One way to accomplish this is with a differential pressure transducer that looks at the difference of pressure across an orifice plate.

We can get volume or mass flow using the following equation

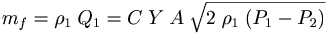
$m_f = \rho_1\;Q_1 = C\;Y\;A\;\sqrt{2\;\rho_1\;(P_1-P_2)}$

where

Q₁ = upstream volumetric flow, m³/s
m_f = mass flow rate at any point, kg/s
C = orifice flow coefficient
Y = expansion factor
A = cross-sectional area of orifice, m²
P₁ = upstream pressure, Pa kg/(m ·s)
P₂ = downstream pressure, Pa kg/(m ·s)
ρ₁ = upstream fluid density, kg/m³

In practice , 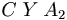$C\;Y\;A_2\;$ become a lumped constant along with any unit scaling- Let's call this constant , 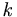$k\;$ then

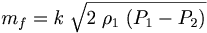
$m_f = k\;\sqrt{2\;\rho_1\;(P_1-P_2)}$

The flow is a constant times the square root of a constant times the pressure difference.

often one can figure out , 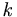$k\;$ and ρ₁ by looking at two known flow rates.

Top Page

wiki Index